Maths

The Story of Maths at Repton Manor Primary School

At Repton Manor Primary School, our intention is that children develop their curiosity about the world through mathematical learning, being met at their starting point, and that they are able to confidently use and apply mathematical concepts in a variety of situations. Children will develop their ability to clearly articulate their ideas, thoughts and reasoning processes, enabling deeper learning. We expect children to make mistakes, and to learn from them, justifying and explaining their methods as they do this. At each stage of learning, children should be able to demonstrate a deep, conceptual understanding of the topic and to be able to build on this over time.

We aim to provide all children with direct teaching every day, which is interactive and stimulating. Our lessons are structured to provide opportunities for children to consolidate their previous learning, use and apply their knowledge, understanding and skills, to pose and ask questions, investigate mathematical ideas, reflect on their own learning and to make links with other work.  A typical lesson will comprise of a starter that helps to reinforce previous learning, a guided practice activity using manipulatives and paired work to support conceptual understanding and this will be followed by independent learning using the ‘White Rose’ programme where appropriate.

What does Maths look like at Repton Manor Primary School?

Implementation

Mastery Curriculum

At Repton Manor Primary School, we follow a Mastery for Maths curriculum, adapting the White Rose programme of study to best meet the needs of our children. We also utilise the Mastering Number enhanced resources provided by the Kent and Medway Maths Hub to ensure that all children are able to deepen their understanding of number, reasoning and problem-solving. This means that children are not streamed by ability because we expect all children to be given the opportunity to achieve age related expectations.  Mastery teaching provides our children with the time to acquire a deep and transferable understanding of mathematical concepts.

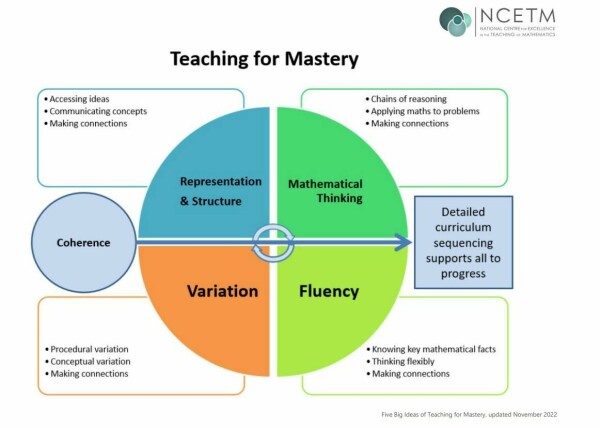
Our Mathematics teaching is underpinned by the Five Big Ideas in Teaching for Mastery:

The Five Big Ideas in Teaching for Mastery:

• Coherence - Teaching is designed to enable a coherent learning progression through the curriculum, providing access for all pupils to develop a deep and connected understanding of mathematics that they can apply in a range of contexts.
• Representation and Structure - Teachers carefully select representations of mathematics to expose mathematical structure. The intention is to support pupils in ‘seeing’ the mathematics, rather than using the representation as a tool to ‘do’ the mathematics. These representations become mental images that students can use to think about mathematics, supporting them to achieve a deep understanding of mathematical structures and connections.
• Mathematical Thinking - Mathematical thinking is central to how pupils learn mathematics and includes looking for patterns and relationships, making connections, conjecturing, reasoning, and generalising. Pupils should actively engage in mathematical thinking in all lessons, communicating their ideas using precise mathematical language.
• Fluency - Efficient, accurate recall of key number facts and procedures is essential for fluency, freeing pupils’ minds to think deeply about concepts and problems, but fluency demands more than this. It requires pupils to have the flexibility to move between different contexts and representations of mathematics, to recognise relationships and make connections, and to choose appropriate methods and strategies to solve problems.
• Variation - The purpose of variation is to draw closer attention to a key feature of a mathematical concept or structure through varying some elements while keeping others constant. Conceptual variation involves varying how a concept is represented to draw attention to critical features. Often more than one representation is required to look at the concept from different perspectives and gain comprehensive knowledge. Procedural variation considers how the student will ‘proceed’ through a learning sequence. Purposeful changes are made in order that pupils’ attention is drawn to key features of the mathematics, scaffolding students’ thinking to enable them to reason logically and make connections.

 

Fluency

We appreciate how important it is for our children to become fluent in all aspects of calculation, therefore, children are offered three opportunities per week to focus on arithmetic/times tables through the use of NumBots and Times Table Rock Stars. Children participate in a Baseline check at the start of each term to assess their progress and are celebrated for their efforts in practicing their number facts as well as for increasing their speedy recall of these facts.

Introducing New Concepts

New concepts will always be introduced with a link back to objectives that the children have already explored.  Children are given many opportunities to make links between embedded and new learning.  Scaffolds (such as new vocabulary and representations) will be included on the Maths Working Wall to support all learners.

Sequence of Learning

Concrete, pictorial, abstract (CPA) is a highly effective approach to teaching Maths that we use which develops a deep and sustainable understanding of Maths.

The Concrete Step of CPA

Concrete is the “doing” stage. During this step, children use objects to model problems. Unlike traditional Maths teaching methods where teachers demonstrate how to solve a problem, the CPA approach brings concepts to life by allowing children to experience and handle physical (concrete) objects. For example, if a problem involves adding pieces of fruit, children can first handle actual fruit. From there, they can progress to handling abstract counters or cubes which represent the fruit.  

The Pictorial Step of CPA

Pictorial is the “seeing” stage. Here, visual representations of concrete objects are used to model problems. This stage encourages children to make a mental connection between the physical object they just handled and the abstract pictures, diagrams or models that represent the objects from the problem.

Building or drawing a model makes it easier for children to grasp difficult abstract concepts (for example, fractions). Simply put, it helps students visualise abstract problems and make them more accessible.

The Abstract step of CPA

Abstract is the “symbolic” stage, where children use abstract symbols to model problems. Children will not progress to this stage until they have demonstrated that they have a solid understanding of the concrete and pictorial stages of the problem. The abstract stage involves the teacher introducing abstract concepts (for example, mathematical symbols). Children are introduced to the concept at a symbolic level, using only numbers, notation, and mathematical symbols (for example, +, –, x, /) to indicate addition, subtraction, multiplication or division.

Although CPA is understood as three distinct stages, our skilled teachers will go back and forth between each stage to reinforce concepts.

Impact

As a result of our Mastery Curriculum and CPA Approach, we are developing:

• Learners who can clearly explain their reasoning and justify their thought processes.

• Quick recall of facts and procedures.

• The flexibility and fluidity to move between different contexts and representations of Mathematics.

• The ability to recognise relationships and make connections between mathematical concepts.

• Happy, confident, articulate and autonomous learners with a life-long passion for learning.

A mathematical concept or skill has been mastered when a child can show it in multiple ways, using the mathematical language to explain their ideas, and can independently apply the concept to new problems in unfamiliar situations.

 

Maths Assessment

Please see the below tabs for our Maths Framework documents and Maths End Points for each year group.

• Maths Framework Documents:
  • Our Maths Framework documents show all of the areas of Maths that children who are working at the expected level at each stage of the year are targeted to achieve.
• Maths End Points:
  • Our Maths End Points show the key objectives that we would like each child to have achieved before moving onto the next year groups curriculum.

If you would like to find out more about Mathematics at Repton Manor Primary School, please contact our Maths Leader, Amanda Bashford.

Curriculum Group: The Sciences

Our Vision:

We aim to build curiosity about our children’s place in the world, how it works and inspire them to look to the future with excitement and the ability to take risks and problem solve.

Through The Sciences curriculum we:

• Give opportunities to interconnect our knowledge, explore and ask why.
• Build strong foundations in subject knowledge.
• Build on successes and failures to find solutions.